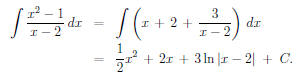Partial Fractions, Long Division

A rational expression is a quotient of polynomials, i.e. has the form

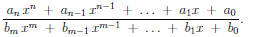
At first sight, rational expressions are difficult to integrate. However, the
algebraic techniques of partial fraction expansion and long division can be used
to make these complex expressions simpler.

1.1 Partial fraction expansion

Word of Warning: Our method here applies when the denominator has linear,
nonrepeated factors only. This will be sufficient for our Calc II class, but some
of you will see more sophisticated methods in other classes.

Partial fractionsworks when the largest power of the numerator is smaller
than the largest power of the denominator. Here are the instructions. Start
with a rational expression:

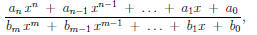
First, completely factor the bottom polynomial:

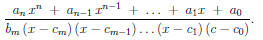
Second, break up the fraction so that the factors of the bottom become the
denominators of individual fractions, with (as of yet) unknown constants in
the numerators:

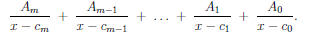
Third, figure out what the constants 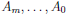are.

Example 1 Use partial fraction expansion to simplify

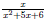
Solution We simply follow the instructions laid out above:
First, factor the bottom:

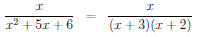
Second, break up the fraction

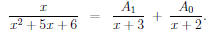
Third, figure out what A₁ and A₀ are:

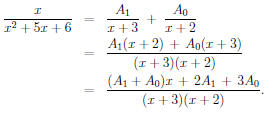
Thus x = (A₁ +A₀)x + 2A₁ + 3A₀, so that A₁ +A₀ = 1 and 2A₁ +3A₀ = 0.
We can solve these two equations, to get A₁ = 3, A₀ = -2. Thus finally

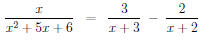
Example 2 Evaluate

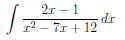
Solution The fraction is too tough to evaluate, so we have to use partial fraction
expansion to simplify it.

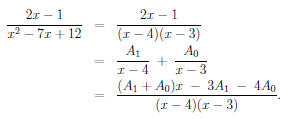
Thus A₁ + A₀ = 2 and -3A₁ - 4A₀ = -1. We can solve this to get A₁ = 7,
A₀ = -5. Therefore

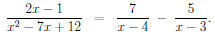
Now we can solve our calculus problem:

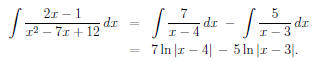
1.2 Long Division

Long division (or synthetic division) can be used when the highest power on
top is equal to or larger than the highest power on bottom.

Example 3 Evaluate

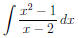
Solution The fraction is too tough to evaluate directly. Since the top power is
bigger, we have to use long division. Using the long division process (which
we discussed in class), we get

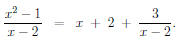
Note: you can also use synthetic division to arrive at this conclusion. Now we
can solve our calculus problem: