Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Calculus I: Sample Exam 4

1. A right circular cylinder is to be designed to hold 22 cubic inches of
coca-cola (approximately 12 fluid ounces). To keep the costs down, we
want to use a minimum of material in the construction. (The volume
of a cylinder is given by V = πr²h:) What if the top costs twice as
much.

2. A rectangular open tank is to have a square base, and its volume is to
be 125 cubic yards. The cost per square yard for the base is $8 and for
the sides is $4. Find the dimensions of the tank in order to minimize
the cost.

3. A box with an open top is to be constructed from a 15" by 24" piece of
cardboard by removing equal size squares from each corner and folding
the resulting flaps upward. The box with the largest volume will have
a height of

4. Solve by horizontal strips only. The area bounded by the curves y =
2 - x² and x + y = 0

5. The area bounded by the lines y = x, x + 2y = 6 and the x axis is:

6. The volume of the solid generated by revolving about the x-axis the
region bounded by the graphs of y = x³; x = 2, and the x-axis.

7. What is the volume of revolution from x = 0 to x = 3/2 when the
function f(x) = 2x² is revolved around the y - axis.

8. The radius of a circle is decreasing at a rate of 0:5 cm per second. At
what rate, in cm² per second, is the circle's area decreasing when the
radius is 4 c

9. A spherical ball of ice with an initial radius of 4 inches melts at a rate
of 2 in³ per minute. How fast is the radius of the ball decreasing when
the radius is 3 inches?

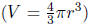
10. The volume of the solid generated by revolving about the x-axis the
region bounded by the graphs of 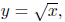x = 0, and y = 2.

11. The volume of the solid generated by revolving about the x-axis the
region bounded by the graphs of x = y² and y = x.