Inverse Functions Facts
If f (g(x)) = x , for all values of x in the domain of g, and g( f (x)) = x ,
for all values of x in the
domain of f, then f and g are called inverse functions. In other words,
if two functions are
inverses, then when the output from either function is used as the input for the
other function, the
result is the same as if nothing had been done to the original input. For
example, if f (2) = 7 and
g(7) = 2, then f (g(7)) = f (2) = 7 and g( f (2)) = g(7) = 2 . The inverse
function of f (x) is usually
denoted f-1(x) .
Notice that if (2,7) is an ordered pair in the function f,
then (7,2) must be an ordered pair in its
inverse function. In other words, the x's and y's of the ordered pairs of the
function f (x) are
interchanged in the ordered pairs of the inverse function f-1(x).So
the domain of f (x) is the range
of f-1(x) and the range of f (x) is the domain of f-1(x)
For example, the domain of f (x) = e^x is
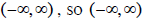 is the range of the inverse of this function.
Similarly, the range of f (x) = e^x is
is the range of the inverse of this function.
Similarly, the range of f (x) = e^x is
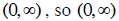 is the domain of the inverse of this
function.
is the domain of the inverse of this
function.
If any y-values in a function are repeated as y-values,
then when the coordinates are interchanged to
produce the inverse function, repeated x-values result and the inverse would not
be a function. A
function that has no repeated y-values is called a one-to-one function
because each x- value has
exactly one corresponding y-value and each y-value has exactly one corresponding
x-value. Only
one-to-one functions have inverses that are functions. Such functions are said
to be invertible. If
we know the graph of a function, we can use the Horizontal Line Test to
determine if the function is
one-to-one.
Horizontal Line Test. If any horizontal line passes
through a graph of a function more than once,
then the function is not one-to-one.
If a function is not one-to-one, we sometimes choose a
one-to-one branch of the function so that an
inverse function is possible. For example,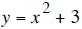 is
not a one-to-one function. However, if we
is
not a one-to-one function. However, if we
restrict the domain to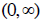 by saying
by saying
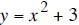 where x ≥ 0,then we have a one-to-one branch
where x ≥ 0,then we have a one-to-one branch
and this function does have an inverse function.
The fact that the x,y pairs in a function and in its
inverse are interchanged suggests a way of finding
the formula for the inverse of a function whose formula is known. Simply
interchange the x's and y's
and solve for the new y. For example, suppose
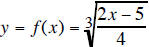
Then to determine the formula for the inverse, we first interchange the x's and y's results in
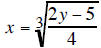
Then to solve for the new y, we cube both sides to get
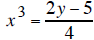
then multiply both sides by 4 to get
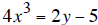 then add
then add
5 to both sides to get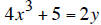 and finally divide both
sides by 2 to get
and finally divide both
sides by 2 to get
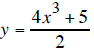
This result is the formula for the inverse function, so
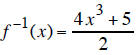
You can verify algebraically, that for
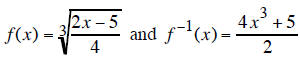
it is indeed true that 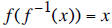 and
and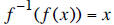 as
required for inverse functions.
as
required for inverse functions.
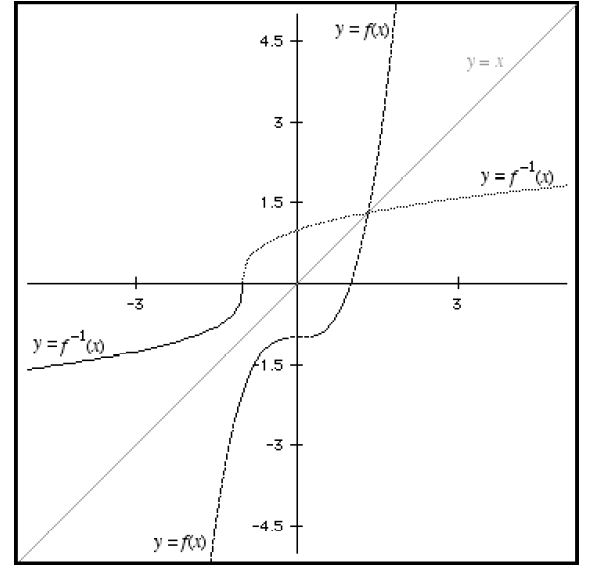
The fact that the x,y pairs in a function and in its
inverse are interchanged also determines how the
graphs of the function and its inverse will be related. The graphs of f(x) and f-1(x)
are symmetric
to each other about the diagonal line y = x. In other words, if both f(x) and f-1(x)
are graphed
on the same coordinate system and the graph is then folded along the diagonal y
= x, the two graphs
will lie exactly on top of each other.