Foundations of Advanced Mathematics

Problem 1

proposition: Let a, b, c, and d be integers. If a|b and c|d then ac|bd.

proof (Direct Proof)

Suppose a, b, c, and d are integers and that a|b and c|d. By definition  of divisibility, there
exist integers x and y such that ax = b and cy = d. Thus, by the associative and commutative
properties of integer multiplication, bd = (ax)(cy) = ac(xy). Since the integers are closed under
multiplication, xy = s for some integer s. Thus, bd = acs, which by definition  implies ac|bd.

Problem 2

proposition: If n is an integer and n^2 is even, then n is even. (Hint: -even is odd)

SCRATH
By the equivalence of the contrapositive, n^2 is even implies n is even i n being odd implies n^2 is odd.

proof (Contrapositive)

Suppose n is an odd integer. By definition, there exists an integer m such that n = 2m + 1.
Thus, by the associative, commutative, and distributive properties, n^2 = (2m+1)^2 = 4m^2+4m+
1 = 2(2m^2+2m)+1. Furthermore, since the integers are closed under addition and multiplication,
2m^2 +2m = s for some integer s. Thus, n^2 = 2s+1. By definition of odd, this implies n^2 is odd.
Thus, by the contrapositive, if n^2 is even, n must be even.

Problem 3

proposition: Let q≥2 be a positive integer. If for all integers a and b, whenever q|ab, q|a or
q|b, then 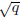is irrational.

proof (Contradiction)

Let q be a positive integer greater than or equal to 2. Suppose that 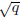is a rational number, and
that for all integers a and b, whenever q|ab, q|a or q|b. We will show this leads to a contradiction.
By definition  of a rational number, 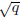can be expressed as n/m where n and m are integers, and
m ≠ 0. Since q ≠ 1, m and n can be chosen in such a way that they do not share any common
factors. Given 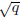= n/m it follows that 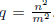. Multiplying both sides of this equation by m^2,
we find n^2 = qm^2. Since the integers are closed under multiplication, m^2 = s for some integer s.
Thus, n^2 = qs, which by definition , implies q|n^2. By our assumption, since q|n^2, q must divide
n. Thus there exists some integer k such that qk = n. Substituting qk in for n in the equation
n^2 = qm^2, and applying the associative and commutative properties of integer multiplication,
we find q^2k^2 = qm^2. By the cancelation law, qk^2 = m^2: Again, by the closure of the integers
under multiplication, there exists some integer t = k^2. Thus qt = m^2, which by definition , implies
q|m^2. By our assumptions, q must also divide m. Thus, q is a common factor of m and n, which
contradicts the fact that m and n were chosen to have no common factors. Therefore, if for all
integers a and b, when q|ab, q|a or q|b, then 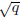must be irrational.

Problem 4: Prove or disprove the following propositions

1. proposition: For each real number x, there exists a real number y such that e^x- y > 0.

proof (Direct Constructive)

Let x be an arbitrary real number. Let y =-exp x. Since the exponential function maps real
numbers to real numbers, clearly y is a real number. Furthermore, e^x- y  = e^x + e^x = 2e^x.
Since 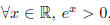, it follows that 2e^x > 0. Thus, since x was an arbitrary real number,
for all real numbers x there exists a real number y such that e^x- y> 0

2. proposition: There exists a real number y such that for all real numbers x, e^x-y > 0.

proof (Direct Constructive)

Let y = 0 and let x be an arbitrary real number. Thus, e^x- y = e^x-0 = e^x. Since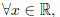
e^x is positive, it follows that e^x > 0. Thus, since x was an arbitrary real number, there
exists a real number y for all real numbers x such that e^x- y > 0