Polynomial Functions

Definition of a Polynomial Function
Let n be a nonnegative integer and let 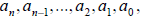be real numbers, with .
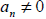The function defined by 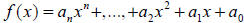is called a polynomial function of x
of degree n. The number a_n , the coefficient of the variable to the highest power, is called the
leading coefficient.

Note: The variable is only raised to positive integer powers–no negative or fractional exponents.
However, the coefficients may be any real numbers, including fractions or irrational numbers
like π or .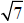

Graph Properties of Polynomial Functions
Let P be any nth degree polynomial function with real coefficients.

The graph of P has the following properties.
1. P is continuous for all real numbers, so there are no breaks, holes, jumps in the graph.
2. The graph of P is a smooth curve with rounded corners and no sharp corners.
3. The graph of P has at most n x-intercepts.
4. The graph of P has at most n – 1 turning points.

Example 1: Given the following polynomial functions, state the leading term, the degree of the
polynomial and the leading coefficient.

a. P(x) = 7x⁴ - 5x³ + x² - 7x + 6

b. P(x) = (3x + 2)(x - 7)² (x + 2)³

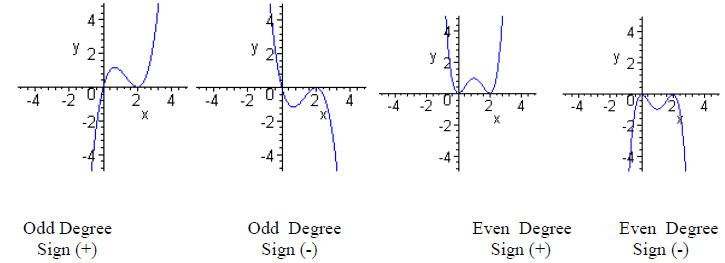
End Behavior of a Polynomial

Odd-degree polynomials look like y = ±x³ .

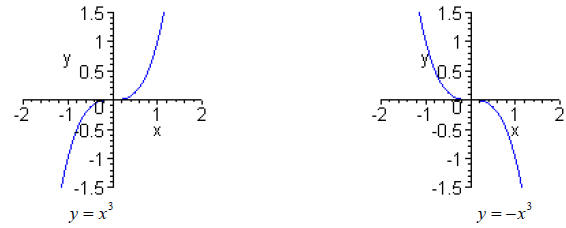
Even-degree polynomials look like y = ±x² .

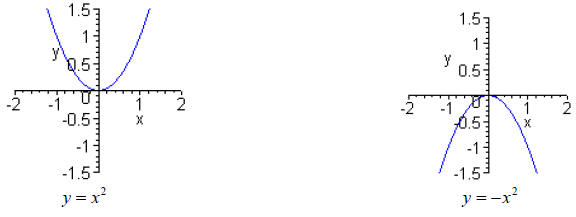
Power functions:
A power function is a polynomial that takes the form f (x) = axⁿ , where n is a positive integer.
Modifications of power functions can be graphed using transformations.
 
 

Even-degree power functions: f (x) = x4	Odd-degree power functions: f (x) = x5

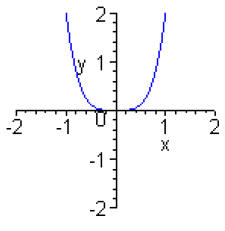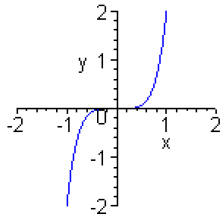Note: Multiplying any function by a will multiply all the y-values by a. The general shape will
stay the same. Exactly the same as it was in section 3.4.

Zeros of a Polynomial

If f is a polynomial and c is a real number for which f (c) = 0, then c is called a zero of f, or a
root of f.
If c is a zero of f, then
· c is an x-intercept of the graph of f.
· (x - c) is a factor of f.
So if we have a polynomial in factored form, we know all of its x-intercepts.
· every factor gives us an x-intercept.
· every x-intercept gives us a factor.

Example 1:
Find the zeros of the polynomial:
P(x) = x³ - 5x² + 6x

Example 2: Consider the function f (x) = -3x(x - 3)⁴ (5x - 2)(2x -1)³(4 - x)² .
Zeros (x-intercepts):
To get the degree, add the multiplicities of all the factors:
The leading term is:

Behavior at Intercepts:
Near an x-intercept, c, the shape of the function is determined by the factor (x-c) and the power
to which it is raised.
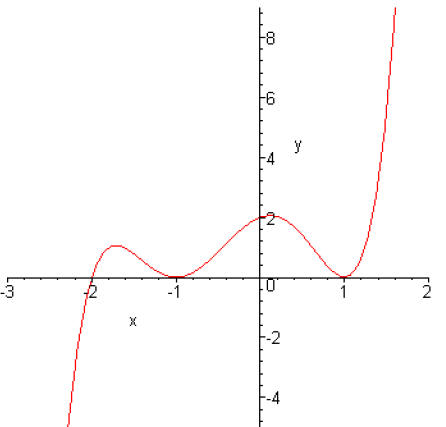
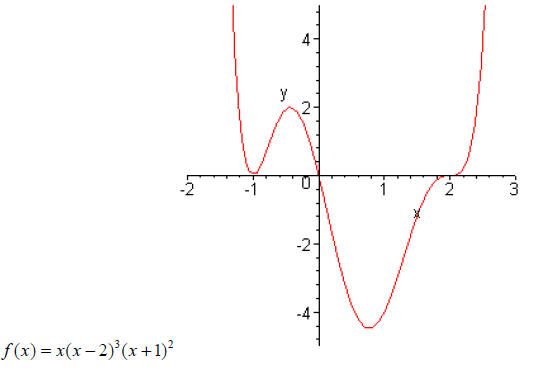
Let’s look again at the graph on the first page

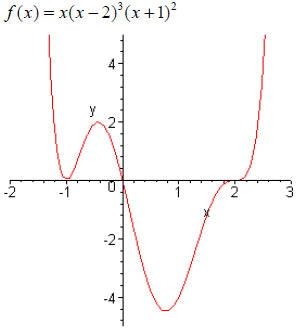
Notice the shape of the graph as it crosses the x-axis at each intercept.
Definition: The multiplicity of a factor in a polynomial function is the power to which it is
raised in the fully factored form of the polynomial. The multiplicity of the factor (x-c) with
no higher power is 1.

Compare the multiplicities of the factors in the above polynomial with the shape at each
corresponding intercept.

The graph of P(x) = (x - c)^k looks like the function f (x) = x^k near the x-intercept c. Since we
know the shape of a power function, we have the following rules:

· Even multiplicity: touches x-axis, but doesn’t cross (looks like a parabola there).
· Odd multiplicity of 1: crosses the x-axis (looks like a line there).
· Odd multiplicity ≥3 : crosses the x-axis and looks like a cubic there.

Steps to graphing other polynomials:
1. Find the y-intercept by finding P(0).
2. Factor and find x-intercepts.
3. Mark x-intercepts on x-axis.
4. For each x-intercept, determine the behavior.
· Even multiplicity: touches x-axis, but doesn’t cross (looks like a parabola there).
· Odd multiplicity of 1: crosses the x-axis (looks like a line there).
· Odd multiplicity ≥3 : crosses the x-axis and looks like a cubic there.
Note: It helps to make a table as shown in the examples below.
5. Determine the leading term.
· Degree: is it odd or even?
· Sign: is the coefficient positive or negative?
6. Determine the end behavior. What does it “look like”?

7. Draw the graph, being careful to make a nice smooth curve with no sharp corners.

Note: without calculus or plotting lots of points, we don’t have enough information to know how
high or how low the turning points are.

Example 3:
Find the zeros then graph the polynomial. Be sure to label the x intercepts, y intercept if
possible and have correct end behavior.

Example 4:
Find the zeros then graph the polynomial. Be sure to label the x intercepts, y intercept if
possible and have correct end behavior.

Example 5:
Find the zeros then graph the polynomial. Be sure to label the x intercepts, y intercept if
possible and have correct end behavior.


Example 6:
Find the zeros then graph the polynomial. Be sure to label the x intercepts, y intercept if
possible and have correct end behavior.



Example 7:
Given the graph of a polynomial determine what the equation of that polynomial.


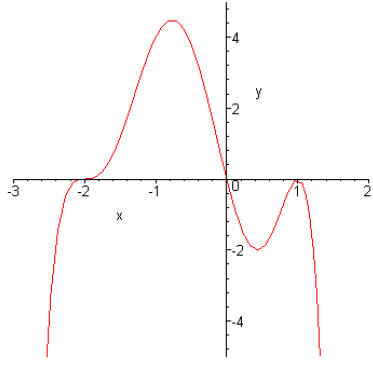
Example 8:
Given the graph of a polynomial determine what the equation of that polynomial.