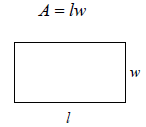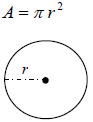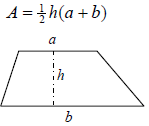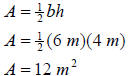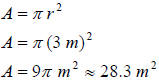Perimeter, Area, and Volume

Geometry comes from the Greek words geo meaning earth and metron meaning measure. Today
we will learn about how to measure certain features of two- and three-dimensional figures that
we see commonly in our everyday world.

Perimeter
The perimeter of a two-dimensional figure is the measure of the distance around that figure.
Perimeter is measured in linear units, such as feet or meters. The perimeter of a straight-line
figure can be calculated by adding the lengths of the sides of the figure. In the example below,
we see that the perimeter is 16.5 meters by totaling the lengths of all five sides.

Example 1: Find the perimeter of the figure.

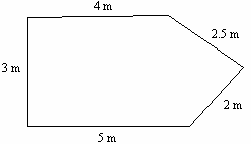
Perimeter of the figure
P = 4 m + 2.5 m + 2 m + 5 m + 3 m
P = 16.5 m
The perimeter of the figure is 16.5 meters.

Rectangles are used frequently enough that we usually refer to a formula instead of the definition
when speaking of their perimeters. The formula for the perimeter of a rectangle is P = 2l + 2w
where l is the length and w is the width of the rectangle. You can easily see why below:

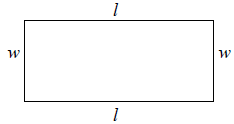
Perimeter of the rectangle
P = l + w + l + w
P = 2l + 2w

A circle is defined as a set of points in the plane that are equally distant from a given point, the
center. The radius of a circle is a line segment from the center to any point on the circle. The
diameter of a circle is a line segment through the center in which its endpoints lie on the circle.

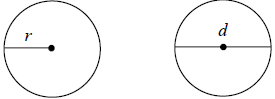
Note: d = 2r

Circumference of a circle
C = π d or C = 2π r

The perimeter of a circle is called its circumference. The circumference of a circle is just over
three times the length of the diameter. More precisely, the circumference is the product of π and
the diameter length, C = π d. It can also be calculated using the radius: C = 2π r. You can
check this out yourself with a can from your kitchen cupboard and a piece of string. Just cut the
string so that its length is one time around the can (circumference). Then count off the diameter
lengths you have within the piece of string by holding it across the top of the can. Regardless of
the size of the can, you will always be able to count off three diameters with a little bit left over.

Example 2: Find the circumference of the circle. Express it in terms of π. Then round to the
nearest tenth.

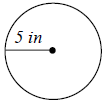
C = 2π r
C = 2π (5 inches)
C = 10π inches
C ≈ 31.4inches

The circumference is exactly 10π inches and approximately 31.4 inches.

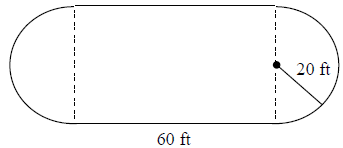
Example 3: Find the perimeter of the figure below in which a rectangle and a semicircle are
joined. (Round to the nearest tenth.)

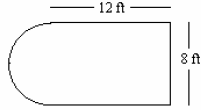
Perimeter = three sides of the rectangle +
the circumference of the semicircle
Perimeter = (12 ft + 8 ft + 12 ft) + ½ [π(8 ft)]
Perimeter = 32 ft + 4π ft
Perimeter ≈ 44.6 feet

The perimeter of the figure is approximately 44.6 feet.

Example 4: (a) Find the perimeter of a rectangle that has a width of 4 yards and a length of 9
yards. (b) Find the circumference of a circle that has a diameter of 12 centimeters.

Example 5: How many plants spaced every 6 inches are needed to surround a circular garden
with a 30-foot radius?

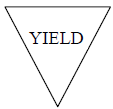
Example 6: The perimeter of a yield sign in the shape of an isosceles triangle is 22 feet. If the
shortest side is 2 feet less than the other two sides, find the length of the shortest
side.

Area
The area of a two-dimensional figure is the measure of the space inside that figure. We measure
the space inside a figure using unit squares. Recall that a square has the same length and width.
The length and width of a unit square are each one.

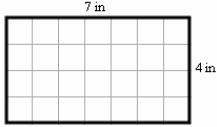
For instance, how many square inches (each square has sides equal to 1 inch) can fit into a
rectangle that has a length of 7 inches and a width of 4 inches as seen in the figure below? A
grid showing square inches has been overlaid on the
rectangle so that we can count the number of squares
contained within it. You may simply count them and find
that the area is 28 square inches. Another way to count the
squares is to notice that there are seven columns of four
squares each. This is a classic multiplication problem.
Seven groups of four can be stated as 7 times 4 yielding an
area of 28 square inches. From this simple example we can see that the area of a rectangle will
be the product of its length and width. We can also find area formulas for other basic two-
dimensional figures:

Rectangle

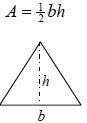
Triangle

Circle

Trapezoid

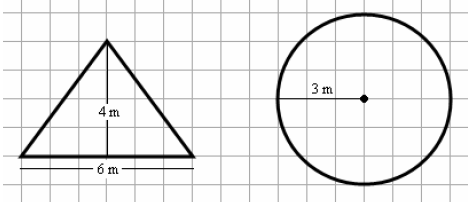
Example 7: (a) Find the area of the following figures using the formula given for its area.
(b) Confirm the area by approximating the number of squares inside the figure.
(Match up partial squares to approximate whole squares.) 

(a) Triangle: The area is 12 square meters.	(a) Circle: The area is ≈28.3 square meters.
(b) There are 6 whole squares and 12 partial squares. Matching up partial squares, we get 6 wholes. Therefore, the area is made up of 12 whole squares. This matches our area in part a.	(b) There are 16 whole square and 20 partial squares. Matching up partial squares, we get about 12 whole squares So the area is made up of about 28 whole squares. This matches up well with the area found in part a.

Example 8: The width of a rectangular garden is 25 feet. The area of the garden is 1250 square
feet. Find the length of the garden.

Example 9: The circumference of a circle is 14π inches. Find the circle’s diameter, radius, and
area.

Example 10: Hardwood flooring costs $10 per square foot. How much will it cost (to the
nearest dollar) to cover the dance floor shown in the figure with hardwood flooring?

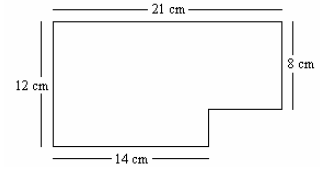
Example 11: Find the area of the figure below.

Volume
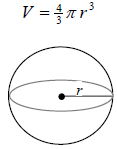
A computer box, a basketball, and soup can are examples of three-dimensional figures. Volume
is the measure of the amount of space inside such an object. Volume is measured using unit
cubes. Recall that a cube has the same length, width, and height. Sugar cubes used in tea or
coffee and alphabet blocks that kids (and adults ☺) play with are examples of cubes.

For instance, consider a box that has a width of 5 inches, a length of 9 inches, and a height of 3
inches. Imagine creating the same size box with inch cubes. How many cubes would make

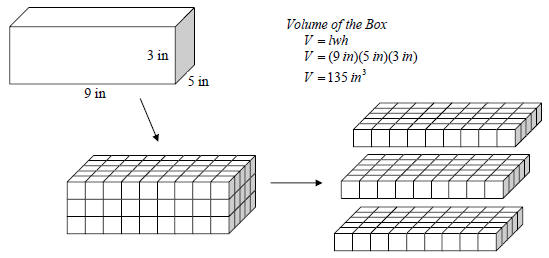
up the box? The box is 3 inches high so there will be 3 layers of cubes within the box. Each
layer contains 5 rows of 9 cubes. So that makes 45 cubes per layer. Since there are 3 layers of
45 cubes each inside the box, the box contains 135 cubes. Thus we conclude that the volume of
the shoe box is 135 cubic inches. Note that we multiplied the length, width, and height together
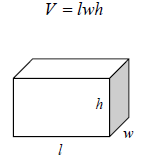
to get the volume of the box. The formula for the volume of a rectangular solid is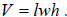
Here are some other common volume formulas:

Rectangular Solid

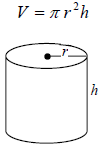
Cylinder

Sphere

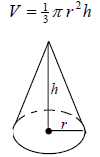
Cone

 

Example 12: Find the volume of soup can that has a height of 12 centimeters and a radius of 4
centimeter.

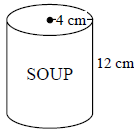
Volume of the Soup Can

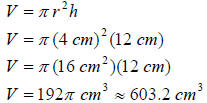
The volume of the soup can is 192π cubic centimeters, approximately 603.2 cubic centimeters.

Example 13: A water storage tank is in the shape of a cone with the pointed end down. If the
radius is 14 feet and the depth of the tank is 15 feet, approximate the volume of the
tank (round to the nearest tenth).

Example 14: A cylindrical fish tank has a diameter of 6 feet and a height of 3 feet. How many
tropical fish can be put in the tank if each fish needs 5 cubic feet of water?

Example 15: Andrea has dug a rectangular foundation 2 meters by 3 meters for a new shed in
her backyard. She has removed 9 cubic meters of dirt. How deep is the hole?